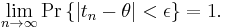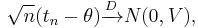Estimator
In statistics, an estimator or point estimate is a statistic (that is, a measurable function of the data) that is used to infer the value of an unknown parameter in a statistical model. The parameter being estimated is sometimes called the estimand. It can be either finite-dimensional (in parametric and semi-parametric models), or infinite-dimensional (semi-nonparametric and non-parametric models). If the parameter is denoted θ then the estimator is typically written by adding a “hat” over the symbol: 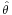 . Being a function of the data, the estimator is itself a random variable; a particular realization of this random variable is called the estimate. Sometimes the words “estimator” and “estimate” are used interchangeably.
. Being a function of the data, the estimator is itself a random variable; a particular realization of this random variable is called the estimate. Sometimes the words “estimator” and “estimate” are used interchangeably.
The definition places virtually no restrictions on which functions of the data can be called the “estimators”. We judge the attractiveness of different estimators by looking at their properties, such as unbiasedness, mean square error, consistency, asymptotic distribution, etc. The construction and comparison of estimators are the subjects of the estimation theory. In the context of decision theory, an estimator is a type of decision rule, and its performance may be evaluated through the use of loss functions.
When the word “estimator” is used without a qualifier, it refers to point estimation. The estimate in this case is a single point in the parameter space. Other types of estimators also exist: interval estimators, where the estimates are subsets of the parameter space; density estimators that deal with estimating the pdfs of random variables, and whose estimates are functions; etc.
Contents |
Definition
Suppose we have a fixed parameter 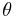 that we wish to estimate. Then an estimator is a function that maps a sample design to a set of sample estimates. An estimator of
that we wish to estimate. Then an estimator is a function that maps a sample design to a set of sample estimates. An estimator of 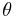 is usually denoted by the symbol
is usually denoted by the symbol 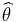 . A sample design can be thought of as an ordered pair
. A sample design can be thought of as an ordered pair 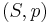 where
where 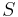 is a set of samples (or outcomes), and
is a set of samples (or outcomes), and 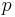 is the probability density function. The probability density function maps the set
is the probability density function. The probability density function maps the set 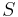 to the closed interval [0,1], and has the property that the sum (or integral) of the values of
to the closed interval [0,1], and has the property that the sum (or integral) of the values of 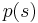 , over all
, over all 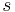 in
in 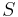 , is equal to 1. For any given subset
, is equal to 1. For any given subset 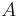 of
of 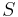 , the sum or integral of
, the sum or integral of 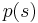 over all
over all 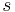 in
in 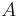 is
is 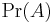 .
.
For all the properties below, the value 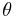 , the estimation formula, the set of samples, and the set probabilities of the collection of samples, can be considered fixed. Yet since some of the definitions vary by sample (yet for the same set of samples and probabilities), we must use
, the estimation formula, the set of samples, and the set probabilities of the collection of samples, can be considered fixed. Yet since some of the definitions vary by sample (yet for the same set of samples and probabilities), we must use 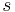 in the notation. Hence, the estimate for a given sample
in the notation. Hence, the estimate for a given sample 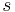 is denoted as
is denoted as 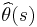 .
.
We have the following definitions and attributes:
- For a given sample
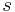 , the error of the estimator
, the error of the estimator 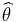 is defined as
is defined as 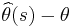 , where
, where 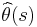 is the estimate for sample
is the estimate for sample 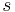 , and
, and 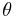 is the parameter being estimated. Note that the error depends not only on the estimator (the estimation formula or procedure), but on the sample.
is the parameter being estimated. Note that the error depends not only on the estimator (the estimation formula or procedure), but on the sample. - The mean squared error of
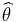 is defined as the expected value (probability-weighted average, over all samples) of the squared errors; that is,
is defined as the expected value (probability-weighted average, over all samples) of the squared errors; that is, ![\operatorname{MSE}(\widehat{\theta}) = \operatorname{E}[(\widehat{\theta} - \theta)^2]](/I/cc3213fe47c74bd456d1c6496503802e.png) . It is used to indicate how far, on average, the collection of estimates are from the single parameter being estimated. Consider the following analogy. Suppose the parameter is the bull's-eye of a target, the estimator is the process of shooting arrows at the target, and the individual arrows are estimates (samples). Then high MSE means the average distance of the arrows from the bull's-eye is high, and low MSE means the average distance from the bull's-eye is low. The arrows may or may not be clustered. For example, even if all arrows hit the same point, yet grossly miss the target, the MSE is still relatively large. Note, however, that if the MSE is relatively low, then the arrows are likely more highly clustered (than highly dispersed).
. It is used to indicate how far, on average, the collection of estimates are from the single parameter being estimated. Consider the following analogy. Suppose the parameter is the bull's-eye of a target, the estimator is the process of shooting arrows at the target, and the individual arrows are estimates (samples). Then high MSE means the average distance of the arrows from the bull's-eye is high, and low MSE means the average distance from the bull's-eye is low. The arrows may or may not be clustered. For example, even if all arrows hit the same point, yet grossly miss the target, the MSE is still relatively large. Note, however, that if the MSE is relatively low, then the arrows are likely more highly clustered (than highly dispersed). - For a given sample
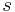 , the sampling deviation of the estimator
, the sampling deviation of the estimator 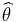 is defined as
is defined as 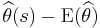 , where
, where 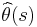 is the estimate for sample
is the estimate for sample 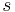 , and
, and 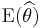 is the expected value of the estimator. Note that the sampling deviation depends not only on the estimator, but on the sample.
is the expected value of the estimator. Note that the sampling deviation depends not only on the estimator, but on the sample. - The variance of
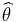 is simply the expected value of the squared sampling deviations; that is,
is simply the expected value of the squared sampling deviations; that is, ![\operatorname{var}(\widehat{\theta}) = \operatorname{E}[(\widehat{\theta} - \operatorname{E}(\widehat{\theta}) )^2]](/I/63c38ec7e1b3491180811540b1aa4087.png) . It is used to indicate how far, on average, the collection of estimates are from the expected value of the estimates. Note the difference between MSE and variance. If the parameter is the bull's-eye of a target, and the arrows are estimates, then a relatively high variance means the arrows are dispersed, and a relatively low variance means the arrows are clustered. Some things to note: even if the variance is low, the cluster of arrows may still be far off-target, and even if the variance is high, the diffuse collection of arrows may still be unbiased. Finally, note that even if all arrows grossly miss the target, if they nevertheless all hit the same point, the variance is zero.
. It is used to indicate how far, on average, the collection of estimates are from the expected value of the estimates. Note the difference between MSE and variance. If the parameter is the bull's-eye of a target, and the arrows are estimates, then a relatively high variance means the arrows are dispersed, and a relatively low variance means the arrows are clustered. Some things to note: even if the variance is low, the cluster of arrows may still be far off-target, and even if the variance is high, the diffuse collection of arrows may still be unbiased. Finally, note that even if all arrows grossly miss the target, if they nevertheless all hit the same point, the variance is zero. - The bias of
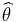 is defined as
is defined as 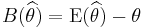 . It is the distance between the average of the collection of estimates, and the single parameter being estimated. It also is the expected value of the error, since
. It is the distance between the average of the collection of estimates, and the single parameter being estimated. It also is the expected value of the error, since 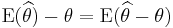 . If the parameter is the bull's-eye of a target, and the arrows are estimates, then a relatively high absolute value for the bias means the average position of the arrows is off-target, and a relatively low absolute bias means the average position of the arrows is on target. They may be dispersed, or may be clustered. The relationship between bias and variance is analogous to the relationship between accuracy and precision.
. If the parameter is the bull's-eye of a target, and the arrows are estimates, then a relatively high absolute value for the bias means the average position of the arrows is off-target, and a relatively low absolute bias means the average position of the arrows is on target. They may be dispersed, or may be clustered. The relationship between bias and variance is analogous to the relationship between accuracy and precision. 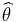 is an unbiased estimator of
is an unbiased estimator of 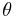 if and only if
if and only if 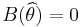 . Note that bias is a property of the estimator, not of the estimate. Often, people refer to a "biased estimate" or an "unbiased estimate," but they really are talking about an "estimate from a biased estimator," or an "estimate from an unbiased estimator." Also, people often confuse the "error" of a single estimate with the "bias" of an estimator. Just because the error for one estimate is large, does not mean the estimator is biased. In fact, even if all estimates have astronomical absolute values for their errors, if the expected value of the error is zero, the estimator is unbiased. Also, just because an estimator is biased, does not preclude the error of an estimate from being zero (we may have gotten lucky). The ideal situation, of course, is to have an unbiased estimator with low variance, and also try to limit the number of samples where the error is extreme (that is, have few outliers). Yet unbiasedness is not essential. Often, if we permit just a little bias, then we can find an estimator with lower MSE and/or fewer outlier sample estimates.
. Note that bias is a property of the estimator, not of the estimate. Often, people refer to a "biased estimate" or an "unbiased estimate," but they really are talking about an "estimate from a biased estimator," or an "estimate from an unbiased estimator." Also, people often confuse the "error" of a single estimate with the "bias" of an estimator. Just because the error for one estimate is large, does not mean the estimator is biased. In fact, even if all estimates have astronomical absolute values for their errors, if the expected value of the error is zero, the estimator is unbiased. Also, just because an estimator is biased, does not preclude the error of an estimate from being zero (we may have gotten lucky). The ideal situation, of course, is to have an unbiased estimator with low variance, and also try to limit the number of samples where the error is extreme (that is, have few outliers). Yet unbiasedness is not essential. Often, if we permit just a little bias, then we can find an estimator with lower MSE and/or fewer outlier sample estimates.- The MSE, variance, and bias, are related:
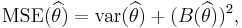 i.e. mean squared error = variance + square of bias. In particular, for an unbiased estimator, the variance equals the MSE.
i.e. mean squared error = variance + square of bias. In particular, for an unbiased estimator, the variance equals the MSE. - The standard deviation of an estimator of θ (the square root of the variance), or an estimate of the standard deviation of an estimator of θ, is called the standard error of θ.
Properties
- Consistency
A consistent sequence of estimators is a sequence of estimators that converge in probability to the quantity being estimated as the index (usually the sample size) grows without bound. In other words, increasing the sample size increases the probability of the estimator being close to the population parameter.
Mathematically, a sequence of estimators 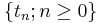 is a consistent estimator for parameter
is a consistent estimator for parameter 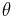 if and only if, for all
if and only if, for all 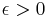 , no matter how small, we have
, no matter how small, we have
The consistency defined above may be called weak consistency. The sequence is strongly consistent, if it converges almost surely to the true value.
An estimator that converges to a multiple of a parameter can be made into a consistent estimator by multiplying the estimator by a scale factor, namely the true value divided by the asymptotic value of the estimator. This occurs frequently in estimation of scale parameters by measures of statistical dispersion.
- Asymptotic normality
An asymptotically normal estimator is a consistent estimator whose distribution around the true parameter 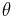 approaches a normal distribution with standard deviation shrinking in proportion to
approaches a normal distribution with standard deviation shrinking in proportion to  as the sample size
as the sample size 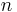 grows. Using
grows. Using 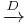 to denote convergence in distribution,
to denote convergence in distribution, 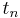 is asymptotically normal if
is asymptotically normal if
for some 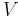 , which is called the asymptotic variance of the estimator.
, which is called the asymptotic variance of the estimator.
The central limit theorem implies asymptotic normality of the sample mean 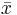 as an estimator of the true mean. More generally, maximum likelihood estimators are asymptotically normal under fairly weak regularity conditions — see the asymptotics section of the maximum likelihood article.
as an estimator of the true mean. More generally, maximum likelihood estimators are asymptotically normal under fairly weak regularity conditions — see the asymptotics section of the maximum likelihood article.
- Efficiency
Two naturally desirable properties of estimators are for them to be unbiased and have minimal mean squared error (MSE). These cannot in general both be satisfied simultaneously: a biased estimator may have lower mean squared error (MSE) than any unbiased estimator: despite having bias, the estimator variance may be sufficiently smaller than that of any unbiased estimator, and it may be preferable to use, despite the bias; see estimator bias.
Among unbiased estimators, there often exists one with the lowest variance, called the minimum variance unbiased estimator (MVUE). In some cases an unbiased efficient estimator exists, which, in addition to having the lowest variance among unbiased estimators, satisfies the Cramér-Rao bound, which is an absolute lower bound on variance for statistics of a variable.
Concerning such "best unbiased estimators", see also Cramér–Rao bound, Gauss–Markov theorem, Lehmann–Scheffé theorem, Rao–Blackwell theorem.
- Robustness
See: Robust estimator, Robust statistics
See also
- Interval estimator
- Best linear unbiased estimator (BLUE)
- Invariant estimator
- Kalman filter
- Markov chain Monte Carlo (MCMC)
- Maximum a posteriori (MAP)
- Median
- Method of moments, generalized method of moments
- Minimum mean squared error (MMSE)
- Particle filter
- Signal Processing
- Testimator
- Wiener filter
- Well-behaved statistic
References
- Lehmann, E. L.; Casella, G. (1998). Theory of Point Estimation (2nd ed.). Springer. ISBN 0-387-98502-6.
- Shao, Jun (1998), Mathematical Statistics, New York: Springer, ISBN 0-387-98674-X
External links
- Weisstein, Eric W., "Estimator" from MathWorld.
- Bol'shev, L.N. (2001), "Statistical Estimator", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/s/s087360.htm
- A maths course on estimators
- Fundamentals of Estimation Theory