Meson
|
|
|
 |
|
|
|
|
| Composition: | Composite—Quarks and antiquarks |
| Particle statistics: | Bosonic |
| Group: | Hadrons |
| Interaction: | Strong |
| Theorized: | Hideki Yukawa (1935) |
| Discovered: | 1947 |
| Types: | ~140 (List) |
| Mass: | From 139 MeV/c2 (π+) to 9,460 MeV/c2 (ϒ) |
| Electric charge: | −1 e, 0 e, +1 e |
| Spin: | 0, 1 |
In particle physics, mesons are subatomic particles composed of one quark and one antiquark. They are part of the hadron particle family—particles made of quarks. The other members of the hadron family are the baryons—subatomic particles composed of three quarks. The main difference between mesons and baryons is that mesons are bosons while baryons are fermions—that is, mesons have integer spin while baryons have half-integer spin—meaning that the Pauli exclusion principle does not apply to mesons.
Since mesons are composed of quarks, they participate in both the weak and strong interactions. Mesons with net electric charge also participate in the electromagnetic interaction. They are classified according to their quark content, total angular momentum, parity, and various other properties such as C-parity and G-parity. While no meson is stable, those of lower mass are nonetheless more stable than the most massive mesons, and are easier to observe and study in particle accelerators or in cosmic ray experiments. They are also typically less massive than baryons, meaning that they are more easily produced in experiments, and will exhibit higher energy phenomena sooner than baryons would. For example, the charm quark was first seen in the J/Psi meson (J/ψ) in 1974,[1][2] and the bottom quark in the upsilon meson (ϒ) in 1977.[3]
Each meson has a corresponding antiparticle (antimeson) where quarks are replaced by their corresponding antiquarks and vice-versa. For example, a positive pion (π+) is made of one up quark and one down antiquark; and its corresponding antiparticle, the negative pion (π−), is made of one up antiquark and one down quark. Some experiments show the evidence of tetraquarks—"exotic" mesons made of two quarks and two antiquarks, but the particle physics community as a whole does not view their existence as likely, although still possible.[4]
Contents |
History
From theoretical considerations, Hideki Yukawa in 1934 predicted the existence of and the approximate mass of the "meson" as the carrier of the nuclear force that holds all atomic nuclei together (except for hydrogen-1). If there was no nuclear force, all nuclei with more than one proton would fly apart because of the electromagnetic repulsion that all of the positively charged protons had upon each other. Yukawa called his predicted particle the meson, from mesos, the Greek word for intermediate, because its predicted mass was between that of the electron and that of the proton, which has about 1,800 times the mass of the electron. Yukawa had originally named his particle the "mesotron", but he was corrected by the physicist Werner Heisenberg (whose father was a professor of Greek at the University of Munich). Heisenberg pointed out that there is no "tr" in the Greek word "mesos".[5]
The first candidate for Yukawa's meson was found quite soon, the "mu meson", or muon that was discovered by Carl David Anderson and others in 1936. The muon had about the right mass to be Yukawa's carrier of the strong nuclear force, but over the course of the next decade, it became more and more clear that the muon was not the right particle. It was eventually found that the muon does not participate in the strong nuclear interaction at all. The muon is actually closely related to the electron and the positron, and they are all actually leptons in today's classification scheme.
There were years of delays in subatomic particle research during World War II in 1939 - 45, with most physicists working in applied projects in radar, the atomic bomb (the Manhattan Project for the U.S.A, the U.K., and Canada), anti-submarine warfare, and more wartime necessities. When the world war ended in August 1945, many physicists gradually returned to peacetime pure research, including in Great Britain.
The first true meson to be discovered was the "pi meson" in 1947, by a team of physicists and others at the University of Bristol in England. The name of this meson was in the course of time contracted to "pion". It also had about the right mass, and over the next few years, more experiments showed that the pion was strongly involved in strong force interactions. The pion (in a virtual state) is the primary carrier particle for the residual strong force (or "nuclear force") that binds nucleons together into atomic nuclei. At least one other meson, the rho meson is involved in mediating this force, as well.
Finally, after many years of delays, in 1949 Dr. Yukawa was awarded the Nobel Prize in Physics for predicting the existence of the meson, and some of its properties.
The word meson has, at times, also been used to mean any force carrier, as in, for instance, the "Z0 meson" which is involved in mediating the weak force, and is not composed of quarks.[6] However, this spurious usage has fallen out of favor. Mesons are now defined as particles composed of pairs of quarks.
Overview
Spin, orbital angular momentum, and total angular momentum
Spin (quantum number S) is a vector quantity that represents the "intrinsic" angular momentum of a particle. It comes in increments of 1⁄2 ħ (pronounced "h-bar"). The ħ is often dropped because it is the "fundamental" unit of spin, and it is implied that "spin 1" means "spin 1 ħ". In some systems of natural units, ħ is chosen to be 1, and therefore does not appear anywhere.
Quarks are fermions, specifically in this case, particles having spin 1⁄2 (S = 1⁄2). Because spin projections varies in increments of 1 (that is 1 ħ), a single quark has a spin vector of length 1⁄2, and has two spin projections (Sz = +1⁄2 and Sz = −1⁄2). Two quarks can have their spins aligned, in which case the two spin vectors add to make a vector of length S = 1 and three spin projections (Sz = +1, Sz = 0, and Sz = −1) called the spin-1 triplet. If two quarks have unaligned spins, the spin vectors add up to make a vector of length S = 0 and has only one spin projection (Sz = 0), called the spin-0 singlet etc. Since mesons are made of one quark and one antiquark, they can be found in triplets and singlets spin states.
There is another quantity of quantized angular momentum, called the orbital angular momentum (quantum number L), that comes in increments of 1 ħ, which represent the angular moment due to quarks orbiting around each other. The total angular momentum (quantum number J) of a particle is therefore the combination of intrinsic angular momentum (spin) and orbital angular momentum. It can take any value from J = |L − S| to J = |L + S|, in increments of 1.
| S | L | J | P (See below) |
JP |
|---|---|---|---|---|
| 0 | 0 | 0 | − | 0− |
| 1 | 1 | + | 1+ | |
| 2 | 2 | − | 2− | |
| 3 | 3 | + | 3+ | |
| 1 | 0 | 1 | − | 1− |
| 1 | 2, 1, 0 | + | 2+, 1+, 0+ | |
| 2 | 3, 2, 1 | − | 3−, 2−, 1− | |
| 3 | 4, 3, 2 | + | 4+, 3+, 2+ |
Particle physicists are most interested in mesons with no orbital angular momentum (L = 0), therefore the two groups of mesons most studied are the S = 1; L = 0 and S = 0; L = 0, which corresponds to J = 1 and J = 0, although they are not the only ones. It is also possible to obtain J = 1 particles from S = 0 and L = 1. How to distinguish between the S = 1, L = 0 and S = 0, L = 1 mesons is an active area of research in meson spectroscopy.
Parity
If the universe were reflected in a mirror, most of the laws of physics would be identical—things would behave the same way regardless of what we call "left" and what we call "right". This concept of mirror reflection is called parity (P). Gravity, the electromagnetic force, and the strong interaction all behave in the same way regardless of whether or not the universe is reflected in a mirror, and thus are said to conserve parity (P-symmetry). However, the weak interaction does distinguish "left" from "right", a phenomenon called parity violation (P-violation).
Based on this, one might think that if the wavefunction for each particle (more precisely, the quantum field for each particle type) were simultaneously mirror-reversed, then the new set of wavefunctions would perfectly satisfy the laws of physics (apart from the weak interaction). It turns out that this is not quite true: In order for the equations to be satisfied, the wavefunctions of certain types of particles have to be multiplied by −1, in addition to being mirror-reversed. Such particle types are said to have negative or odd parity (P = −1, or alternatively P = –), while the other particles are said to have positive or even parity (P = +1, or alternatively P = +).
For mesons, the parity is related to the orbital angular momentum by the relation:[7]
where the L is a result of the parity of the corresponding spherical harmonic of the wavefunction. The '+1' in the exponent comes from the fact that, according to the Dirac equation, a quark and an antiquark have opposite intrinsic parities. Therefore the intrinsic parity of a meson is the product of the intrinsic parities of the quark (+1) and antiquark (−1). As these are different, their product is −1, and so it contributes a +1 in the exponent.
As a consequence, mesons with no orbital angular momentum (L = 0) all have odd parity (P = −1).
C-parity
C-parity is only defined for mesons that are their own antiparticle (i.e. neutral mesons). It represents whether or not the wavefunction of the meson remains the same under the interchange of their quark with their antiquark.[8] If
then, the meson is "C even" (C = +1). On the other hand, if
then the meson is "C odd" (C = −1).
C-parity rarely is studied on its own, but the combination of C- and P-parity into CP-parity. CP-parity was thought to be conserved, but was later found to be violated in weak interactions.[9][10][11]
G-parity
G parity is a generalizations of the C-parity. Instead of simply comparing the wavefunction after exchanging quarks and antiquarks, it compares the wavefunction after exchanging the meson for the corresponding antimeson, regardless of quark content.[12] In the case of neutral meson, G-parity is equivalent to C-parity because neutral mesons are their own antiparticles.
If
then, the meson is "G even" (G = +1). On the other hand, if
then the meson is "G odd" (G = −1).
Isospin and charge

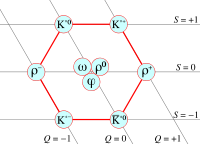
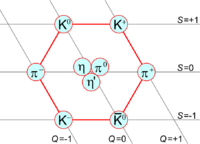
The concept of isospin was first proposed by Werner Heisenberg in 1932 to explain the similarities between protons and neutrons under the strong interaction.[13] Although they had different electric charges, their masses were so similar that physicists believed they were actually the same particle. The different electric charges were explained as being the result of some unknown excitation similar to spin. This unknown excitation was later dubbed isospin by Eugene Wigner in 1937.[14] When the first mesons were discovered, they too were seen through the eyes of isospin. The three pions were believed to be the same particle, but in different isospin states.
This belief lasted until Murray Gell-Mann proposed the quark model in 1964 (containing originally only the u, d, and s quarks).[15] The success of the isospin model is now understood to be the result of the similar masses of the u and d quarks. Since the u and d quarks have similar masses, particles made of the same number then also have similar masses. The exact specific u and d quark composition determines the charge, as u quarks carry charge +2⁄3 while d quarks carry charge −1⁄3. For example the three pions all have different charges (π+ (ud), π0 (a quantum superposition of uu and dd states), π− (du)), but have similar masses (~140 MeV/c2) as they are each made of a total of pairs of up and down quarks and antiquarks. Under the isospin model, they were considered to be a single particle in different charged states.
The mathematics of isospin was modeled after that of spin. Isospin projections varied in increments of 1 just like those of spin, and to each projection was associated a "charged state". Since the "pion particle" had three "charged states", it was said to be of isospin I = 1. Its "charged states" π+, π0, and π−, corresponded to the isospin projections I3 = +1, I3 = 0, and I3 = −1 respectively. Another example is the "rho particle", also with three charged states. Its "charged states" ρ+, ρ0, and ρ−, corresponded to the isospin projections I3 = +1, I3 = 0, and I3 = −1 respectively. It was later noted that the isospin projections were related to the up and down quark content of particles by the relation
where the n's are the number of up and down quarks and antiquarks.
In the "isospin picture", the three pions and three rhos were thought to be the different states of two particles. However in the quark model, the rhos are excited states of pions. Isospin, although conveying an inaccurate picture of things, is still used to classify hadrons, leading to unnatural and often confusing nomenclature. Since mesons are hadrons, the isospin classification is also used, with I3 = +1⁄2 for up quarks and down antiquarks, and I3 = −1⁄2 for up antiquarks and down quarks.
Flavour quantum numbers
The strangeness flavour quantum number S (not to be confused with spin) was noticed to go up and down along with particle mass. The higher the mass, the lower the strangeness (the more s quarks). Particles could be described with isospin projections (related to charge) and strangeness (mass) (see the uds nonet figures on the right). As other quarks were discovered, new quantum numbers were made to have similar description of udc and udb nonets. Since only the u and d mass are similar, this description of particle mass and charge in terms of isospin and flavour quantum numbers only works well for the nonets made of one u, one d and one other quark and breaks down for the nonets (for example ucb nonet). If the quarks all had the same mass, their behaviour would be called symmetric, as they would all behave in exactly the same way with respect to the strong interaction. Since quarks do not have the same mass, they do not interact in the same way (exactly like an electron placed in an electric field will accelerate more than a proton placed in the same field because of its lighter mass), and the symmetry is said to be broken.
It was noted that charge (Q) was related to the isospin projection (I3), the baryon number (B) and flavour quantum numbers (S, C, B′, T) by the Gell-Mann–Nishijima formula:[16]
where S, C, B′, and T represent the strangeness, charmness, bottomness and topness flavour quantum numbers respectively. They are related to the number of strange, charm, bottom, and top quarks and antiquark according to the relations:
meaning that the Gell-Man–Nishijima formula is equivalent to the expression of charge in terms of quark content:
Classification
Mesons are classified into groups according to their isospin (I), total angular momentum (J), parity (P), G-parity (G) or C-parity (C) when applicable, and quark (q) content. The rules for classification are defined by the Particle Data Group, and are rather convoluted.[17] The rules are presented below, in table form for simplicity.
Types of meson
Mesons are classified into types according to their spin configurations. Some specific configurations are given special names based on the mathematical properties of their spin configuration.
| Type | S | L | P | J | JP |
|---|---|---|---|---|---|
| Pseudoscalar meson | 0 | 0 | − | 0 | 0− |
| Pseudovector meson | 0 | 1 | + | 1 | 1+ |
| Vector meson | 1 | 0 | − | 1 | 1− |
| Scalar meson | 1 | 1 | + | 0 | 0+ |
| Tensor meson | 1 | 1 | + | 2 | 2+ |
Nomenclature
Flavourless mesons
Flavourless mesons are mesons made of pair of quark and antiquarks of the same flavour (all their flavour quantum numbers are zero: I3 = 0, S = 0, C = 0, B′ = 0, T = 0). The rules for flavourless mesons are:[17]
| qq content | J PC†→ I ↓ |
0−+, 2−+, 4−+, ... | 1+−, 3+−, 5+−, ... | 1−−, 2−−, 3−−, ... | 0++, 1++, 2++, ... |
|---|---|---|---|---|---|
ud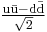 du |
1 | π+ π0 π− |
b+ b0 b− |
ρ+ ρ0 ρ− |
a+ a0 a− |
| Mix of uu, dd, ss | 0 | η η′ |
h h′ |
ω φ |
f f′ |
| cc | 0 | ηc | hc | ψ†† | χc |
| bb | 0 | ηb | hb | ϒ | χb |
| tt | 0 | ηt | ht | θ | χt |
† ^ The C parity is only relevant to neutral mesons.
†† ^ For JPC=1−−, the ψ is often called the J/ψ
In addition:
- When the spectroscopic state of the meson is known, it is added in parenthesis.
- When the spectroscopic state is unknown, mass (in MeV/c2) is added in parenthesis.
- When the meson is in its ground state, nothing is added in parenthesis.
Flavourful mesons
Flavourful mesons are mesons made of pair of quark and antiquarks of different flavours. The rules are simpler in this case: the main symbol depends on the heavier quark, the superscript depends on the charge, and the subscript (if any) depends on the lighter quark. In table form, they are:[17]
| antiquark → quark ↓ |
up | down | charm | strange | top | bottom |
|---|---|---|---|---|---|---|
| up | — | — | D0 | K+ | T0 | B+ |
| down | — | — | D− | K0 | T− | B0 |
| charm | D0 | D+ | — | D+s | T0c | B+c |
| strange | K− | K0 | D−s | — | T+s | B0s |
| top | T0 | T+ | T0c | T−s | — | T−b |
| bottom | B− | B0 | B−c | B0s | T+b | — |
In addition:
- If JP is in the "normal series" (i.e., JP = 0+, 1−, 2+, 3−, ...), a superscript ∗ is added.
- If the meson is not pseudoscalar (JP = 0-) or vector (JP = 1−), J is added as a subscript.
- When the spectroscopic state of the meson is known, it is added in parenthesis.
- When the spectroscopic state is unknown, mass (in MeV/c2) is added in parenthesis.
- When the meson is in its ground state, nothing is added in parenthesis.
List
See also
Notes
- ↑ J.J. Aubert et al. (1974)
- ↑ J.E. Augustin et al. (1974)
- ↑ S.W. Herb et al. (1977)
- ↑ C. Amsler et al. (2008): Charmonium States
- ↑ [1], The great physicists from Galileo to Einstein
- ↑ J. Steinberger (1998)
- ↑ C. Amsler et al. (2008): Quark Model
- ↑ M.S. Sozzi (2008b)
- ↑ J.W. Cronin (1980)
- ↑ V.L. Fitch (1980)
- ↑ M.S. Sozzi (2008c)
- ↑ K. Gottfried, V.F. Weisskopf (1986)
- ↑ W. Heisenberg (1932)
- ↑ E. Wigner (1937)
- ↑ M. Gell-Mann (1964)
- ↑ S.S.M Wong (1998)
- ↑ 17.0 17.1 17.2 C. Amsler et al. (2008): Naming scheme for hadrons
- ↑ W.E. Burcham, M. Jobes (1995)
References
- M.S. Sozzi (2008a). "Parity". Discrete Symmetries and CP Violation: From Experiment to Theory. Oxford University Press. pp. 15–87. ISBN 0199296669.
- M.S. Sozzi (2008b). "Charge Conjugation". Discrete Symmetries and CP Violation: From Experiment to Theory. Oxford University Press. pp. 88–120. ISBN 0199296669.
- M.S. Sozzi (2008c). "CP-Symmetry". Discrete Symmetries and CP Violation: From Experiment to Theory. Oxford University Press. pp. 231–275. ISBN 0199296669.
- C. Amsler et al. (Particle Data Group) (2008). "Review of Particle Physics". Physics Letters B 667 (1): 1–1340. doi:10.1016/j.physletb.2008.07.018.
- S.S.M. Wong (1998). "Nucleon Structure". Introductory Nuclear Physics (2nd ed.). New York (NY): John Wiley & Sons. pp. 21–56. ISBN 0-471-23973-9.
- W.E. Burcham, M. Jobes (1995). Nuclear and Particle Physics (2nd ed.). Longman Publishing. ISBN 0-582-45088-8.
- R. Shankar (1994). Principles of Quantum Mechanics (2nd ed.). New York (NY): Plenum Press. ISBN 0-306-44790-8.
- J. Steinberger (1989). "Experiments with high-energy neutrino beams". Reviews of Modern Physics 61 (3): 533–545. doi:10.1103/RevModPhys.61.533.
- K. Gottfried, V.F. Weisskopf (1986). "Hadronic Spectroscopy: G-parity". Concepts of Particle Physics. 2. Oxford University Press. pp. 303–311. ISBN 0195033930.
- J.W. Cronin (1980). "CP Symmetry Violation—The Search for its origin". The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1980/cronin-lecture.pdf.
- V.L. Fitch (1980). "The Discovery of Charge—Conjugation Parity Asymmetry". The Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1980/fitch-lecture.pdf.
- S.W. Herb et al. (1977). "Observation of a Dimuon Resonance at 9.5 Gev in 400-GeV Proton-Nucleus Collisions". Physical Review Letters 39 (5): 252–255. doi:10.1103/PhysRevLett.39.252.
- J.J. Aubert et al. (1974). "Experimental Observation of a Heavy Particle J". Physical Review Letters 33 (23): 1404–1406. doi:10.1103/PhysRevLett.33.1404.
- J.E. Augustin et al. (1974). "Discovery of a Narrow Resonance in e+e− Annihilation". Physical Review Letters 33 (23): 1406–1408. doi:10.1103/PhysRevLett.33.1406.
- M. Gell-Mann (1964). "A Schematic of Baryons and Mesons". Physics Letters 8 (3): 214–215. doi:10.1016/S0031-9163(64)92001-3.
- E. Wigner (1937). "On the Consequences of the Symmetry of the Nuclear Hamiltonian on the Spectroscopy of Nuclei". Physical Review 51 (2): 106–119. doi:10.1103/PhysRev.51.106.
- W. Heisenberg (1932). "Über den Bau der Atomkerne I". Zeitschrift für Physik 77: 1–11. doi:10.1007/BF01342433. (German)
- W. Heisenberg (1932). "Über den Bau der Atomkerne II". Zeitschrift für Physik 78: 156–164. doi:10.1007/BF01337585. (German)
- W. Heisenberg (1932). "Über den Bau der Atomkerne III". Zeitschrift für Physik 80: 587–596. doi:10.1007/BF01335696. (German)
External links
- A table of some mesons and their properties
- Particle Data Group—Compiles authoritative information on particle properties
- hep-ph/0211411: The light scalar mesons within quark models
- Naming scheme for hadrons (a PDF file)
Recent findings
- What Happened to the Antimatter? Fermilab's DZero Experiment Finds Clues in Quick-Change Meson
- CDF experiment's definitive observation of matter-antimatter oscillations in the Bs meson
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
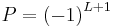

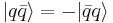

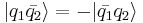
![I_3=\frac{1}{2}[(n_u-n_\bar{u})-(n_d-n_\bar{d})],](/I/f65234fbb4924c8bf4a64738cb7232d4.png)
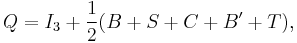
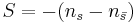
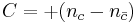

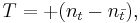
![Q=\frac{2}{3}[(n_u-n_\bar{u})+(n_c-n_\bar{c})+(n_t-n_\bar{t})]-\frac{1}{3}[(n_d-n_\bar{d})+(n_s-n_\bar{s})+(n_b-n_\bar{b})].](/I/05a31d0bf1102cc058076081a3bf734c.png)