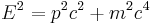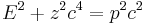Tachyon

Quantum field theory

(Feynman diagram)

History of... Background Gauge theory Field theory Poincaré symmetry Quantum mechanics Spontaneous symmetry breaking Symmetries Crossing Charge conjugation Parity Time reversal Tools Anomaly Effective field theory Expectation value Faddeev–Popov ghosts Feynman diagram Lattice gauge theory LSZ reduction formula Partition function Propagator Quantization Renormalization Vacuum state Wick's theorem Wightman axioms Equations Dirac equation Klein–Gordon equation Proca equations Wheeler–DeWitt equation Standard Model Electroweak interaction Higgs mechanism Quantum chromodynamics Quantum electrodynamics Yang–Mills theory Incomplete theories Quantum gravity String theory Supersymmetry Technicolor Theory of everything Scientists Adler • Bethe • Bogoliubov • Callan • Candlin • Coleman • DeWitt • Dirac • Dyson • Fermi • Feynman • Fierz • Fröhlich • Gell-Mann • Goldstone • Gross • 't Hooft • Jackiw • Klein • Landau • Lee • Lehmann • Majorana • Nambu • Parisi • Polyakov • Salam • Schwinger • Skyrme • Stueckelberg •Symanzik • Tomonaga • Veltman • Weinberg • Weisskopf • Wilson • Wilczek • Witten • Yang • Yukawa • Zimmermann • Zinn-Justin

A tachyon (pronounced /ˈtæki.ɒn/; Greek: ταχύς, takhus, "swift" + English: -on "elementary particle") is a hypothetical subatomic particle that moves faster than light. In the language of special relativity, a tachyon is a particle with space-like four-momentum and imaginary proper time. A tachyon is constrained to the space-like portion of the energy-momentum graph. Therefore, it cannot slow down to subluminal speeds.

The first description of tachyons is attributed to German physicist Arnold Sommerfeld. However, it was George Sudarshan,^[1] Olexa-Myron Bilaniuk,^[2] Vijay Deshpande,^[2] and Gerald Feinberg^[3] (who originally coined the term in the 1960s) who advanced a theoretical framework for their study.

If tachyons were conventional, localizable particles that could be used to send signals faster than light, this would lead to violations of causality in special relativity. But in the framework of quantum field theory, tachyons are understood as signifying an instability of the system and treated using tachyon condensation, rather than as real faster-than-light particles, and such instabilities are described by tachyonic fields. Tachyonic fields have appeared theoretically in a variety of contexts, such as the bosonic string theory. According to the contemporary and widely accepted understanding of the concept of a particle, tachyon particles are too unstable to be treated as existent.^[4] By that theory, faster than light information transmission and causality violation with tachyons are impossible.

Conventional massive particles which travel slower than the speed of light are sometimes termed "bradyons" or "tardyons" in contrast, although these terms are only used in the context of discussions about tachyons.

Because a tachyon moves faster than the speed of light, we cannot see it approaching. After a tachyon has passed nearby, we would be able to see two images of it, appearing and departing in opposite directions. The black line is the shock wave of Cherenkov radiation, shown only in one moment of time. This double image effect is most prominent for an observer located directly in the path of a superluminal object (in this example a sphere, shown in grey). The right hand bluish shape is the image formed by the blue-doppler shifted light arriving at the observer—who is located at the apex of the black Cherenkov lines—from the sphere as it approaches. The left-hand reddish image is formed from redshifted light that leaves the sphere after it passes the observer. Because the object arrives before the light, the observer sees nothing until the sphere starts to pass the observer, after which the image-as-seen-by-the-observer splits into two—one of the arriving sphere (to the right) and one of the departing sphere (to the left).

Despite the theoretical arguments against the existence of tachyon particles, experimental searches have been conducted to test the assumption against their existence; however, no experimental evidence for the existence of tachyon particles has been found.^[5]

Properties

From a special relativity dynamics perspective a tachyon is a particle with space-like four-momentum. The existence of such particles would pose intriguing problems in modern physics.

Mass

There are two equivalent approaches to handling their kinematics:

• Requires that all the same formulas that apply to regular slower-than-light particles ("bradyons") also apply to tachyons. In particular the energy-momentum relation:

where p is the relativistic momentum of the bradyon and m is its rest mass still holds, along with the formula for the total energy of a particle:

which is interpreted to mean that the total energy of a particle (bradyon or tachyon) contains a contribution from the rest mass (the "rest mass-energy") and a contribution from the body's motion, the kinetic energy.

However the energy equation has, when v is larger than c, an "imaginary" denominator, as the value inside the square root is negative. Because the total energy must be real then the numerator must also be imaginary (i.e., the rest mass m must be imaginary, as a pure imaginary number divided by another pure imaginary number is a real number).

In quantum field theory imaginary mass would induce tachyon condensation.

• A simple substitution for the mass yields an equivalent way of describing tachyons with real masses. Define m = i*z (where 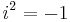) and we get Einstein's energy-momentum relation to read:

With this approach the energy equation becomes:

And we avoid any necessity for imaginary masses, sidestepping the problem of interpreting exactly what a complex-valued mass may physically mean. Except, of course, when converting z back to m for interactions with non-tachyon particles. Both approaches are equivalent mathematically and have the same physical consequences.

Speed

One curious effect is that, unlike ordinary particles, the speed of a tachyon increases as its energy decreases. (For ordinary bradyonic matter, E increases with increasing speed, becoming arbitrarily large as v approaches c, the speed of light.) Therefore, just as bradyons are forbidden to break the light-speed barrier, so too are tachyons forbidden from slowing down to below c, because infinite energy is required to reach the barrier from either above or below.

As noted by Gregory Benford et al., among others, special relativity implies that tachyons, if they existed, could be used to communicate backwards in time^[6] (see Tachyonic antitelephone article). Since time travel is considered to be non-physical, tachyons are believed by physicists to either not exist, or else to be incapable of interacting with normal matter.

Cherenkov radiation

Taking the formalisms of electromagnetic radiation and supposing a tachyon had an electric charge—as there is no reason to suppose a priori that tachyons must be either neutral or charged—then a charged tachyon must lose energy as Cherenkov radiation^[7]—just as ordinary charged particles do when they exceed the local speed of light in a medium. A charged tachyon traveling in a vacuum therefore undergoes a constant proper time acceleration and, by necessity, its worldline forms a hyperbola in space-time. However, as we have seen, reducing a tachyon's energy increases its speed, so that the single hyperbola formed is of two oppositely charged tachyons with opposite momenta (same magnitude, opposite sign) which annihilate each other when they simultaneously reach infinite speed at the same place in space. (At infinite speed the two tachyons have no energy each and finite momentum of opposite direction, so no conservation laws are violated in their mutual annihilation. The time of annihilation is frame dependent.) Even an electrically neutral tachyon would be expected to lose energy via gravitational Cherenkov radiation, because it has a gravitational mass, and therefore increase in speed as it travels, as described above.

Quantum field theory

Quantizing tachyons shows that they must be spinless particles which obey Fermi-Dirac statistics; i.e., tachyons are Scalar fermions, a combination which is not permitted for ordinary particles.^[3] They also must be created and annihilated in pairs.

Causality

The property of causality is a fundamental principle of theoretical particle physics. If tachyons could be used to transmit information faster than light, then according to relativity they could also be used to violate causality using a scheme sometimes known as the "tachyon telephone paradox".^[8] This can be understood in terms of the relativity of simultaneity in special relativity, which says that in some cases different inertial reference frames will disagree on whether two events at different locations happened "at the same time" or not, and they can also disagree on the order of the two events (technically, these disagreements occur when spacetime interval between the events is 'space-like', meaning that neither event lies in the future light cone of the other).^[9]

If one of the two events represents the sending of a signal from one location and the second event represents the reception of the same signal at another location, then as long as the signal is moving at the speed of light or slower, the mathematics of simultaneity ensures that all reference frames agree that the transmission-event happened before the reception-event.^[9] However, in the case of a hypothetical signal moving faster than light, there would always be some frames in which the signal was received before it was sent, so that the signal could be said to have moved backwards in time. And because one of the two fundamental postulates of special relativity says that the laws of physics should work the same way in every inertial frame, then if it is possible for signals to move backwards in time in any one frame, it must be possible in all frames. This means that if observer A sends a signal to observer B which moves faster than light in A's frame but backwards in time in B's frame, and then B sends a reply which moves faster than light in B's frame but backwards in time in A's frame, it could work out that A receives the reply before sending the original signal, a clear violation of causality in every frame. Mathematical details can be found in the tachyonic antitelephone article, and an illustration of such a scenario using spacetime diagrams can be found here.

It has been argued that we can avoid the notion of tachyons traveling into the past using the Feinberg reinterpretation principle^[3] which states that a negative-energy tachyon sent back in time in an attempt to violate causality can always be reinterpreted as a positive-energy tachyon traveling forward in time. This is because observers cannot distinguish between the emission and absorption of tachyons. For a tachyon, there is no distinction between the processes of emission and absorption, because there always exists a sub-light speed reference frame shift that alters the temporal direction of the tachyon's world-line, which is not true for bradyons or luxons. The attempt to detect a tachyon from the future (and violate causality) can actually create the same tachyon and sends it forward in time (which is causal).

According to the Feinberg reinterpretation principle every tachyon detector will register tachyons in every possible detection mode; from the perspective of a frame where the registration by the "detector" preceded the activation of the "emitter", the "detector" in the past is actually spontaneously emitting tachyons, only some of which will be intercepted by the detector in the future. However, Feinberg's reinterpretation principle, which simply relabels the events so that the earlier event is defined as the "emission" and the later one the "detection", does not in itself solve the causality problems associated with tachyon information transmission.^[8] For example, suppose experimenter A could selectively influence the rate at which tachyons from her emitter traveled to the detector of experimenter B, and B could measure changes in the rate tachyons arrived at his detector, so that A could transmit a message to B in binary code. Then in a frame where B's detector went off at an earlier time than A influenced her emitter, merely relabeling B's device as a "spontaneous emitter" and A's as a "detector" wouldn't change the fact that B, by observing the changing rates of tachyons being spontaneously emitted from his device, could gain information about A's interactions with her own device in the future. Only in the case where it was impossible to influence tachyon emissions in such a way as to transmit information would Feinberg's reinterpretation principle fully resolve the issues with causality.

In fact, there are arguments from quantum field theory suggesting that even if tachyons existed, they could not be used to transmit information faster than light at all, either because disturbances in the quantum field for a tachyon would not actually propagate faster than light, or because the tachyon is impossible to localize.^[10] Without the possibility of faster-than-light information transmission, the problem of backwards-in-time information transmission could be avoided as well.

In the theory of general relativity, it is possible to construct spacetimes in which particles travel faster than the speed of light, relative to a distant observer. One example is the Alcubierre metric, another is of traversable wormholes. However, these are not tachyons in the above sense, as they do not exceed the speed of light locally.

Condensation

In quantum field theory, a tachyon is a quantum of a field—usually a scalar field—whose squared mass is negative, and is used to describe spontaneous symmetry breaking: The existence of such a field implies the instability of the field vacuum; the field is at a local maximum rather than a local minimum of its potential energy, much like a ball at the top of a hill. A very small impulse (which will always happen due to quantum fluctuations) will lead the field to roll down with exponentially increasing amplitudes: it will induce tachyon condensation. It is important to realize that once the tachyonic field reaches the minimum of the potential, its quanta are not tachyons any more but rather have a positive mass-squared, such as the Higgs boson.

Technically, the squared mass is the second derivative of the effective potential, at a point where the first derivative is zero. So for a tachyonic field the second derivative is negative, meaning that the effective potential is at a local maximum rather than a local minimum. Therefore this situation is unstable and the field will roll down to another point, stopping only at a local minimum, where its quanta have a non-negative squared mass, so that it is not tachyonic any longer.^[4]

Because a tachyon's squared mass is negative, it formally has an imaginary mass. This is a special case of the general rule, where unstable massive particles are formally described as having a complex mass, with the real part being their mass in usual sense, and the imaginary part being the decay rate in natural units.^[4]

However, in quantum field theory, a particle (a "one-particle state") is roughly defined as a state which is constant over time; i.e., an eigenvalue of the Hamiltonian. An unstable particle is a state which is only approximately constant over time; However, it exists long enough to be measured. This means that if it is formally described as having a complex mass, then the real part of the mass must be greater than its imaginary part. If both parts are of the same magnitude, this is considered a resonance appearing in a scattering process rather than particle, as it does not exist long enough to be measured independently of the scattering process. In the case of a tachyon, the imaginary part of the mass is infinitely larger than the real part, and hence no concept of a particle can be attributed to it.

It is important to stress that even for tachyonic quantum fields, the field operators at spacelike separated points still commute (or anticommute), thus preserving causality. Therefore information never moves faster than light.

Examples for tachyonic fields are all cases of spontaneous symmetry breaking. In condensed matter physics a notable example is ferromagnetism; in particle physics the best known example is the Higgs mechanism in the standard model.

Tachyons in string theory

In string theory tachyons have the same interpretation as in quantum field theory. However, string theory can, at least in principle, not only describe the physics of tachyonic fields, but also predict whether such fields appear.

Tachyonic fields indeed arise in many versions of string theory. In general, string theory states that what we see as "particles"—electrons, photons, gravitons and so forth—are actually different vibrational states of the same underlying string. The mass of the particle can be deduced from the vibrations which the string exhibits; roughly speaking, the mass depends upon the "note" which the string sounds. Tachyons frequently appear in the spectrum of permissible string states, in the sense that some states have negative mass-squared, and therefore imaginary mass. If the tachyon appears as a vibrational mode of an open string, this signals an instability of the underlying D-brane system to which the string is attached.^[11] The system will then decay to a state of closed strings and/or stable D-branes. If the tachyon is a closed string vibrational mode, this indicates an instability in spacetime itself. Generally, it is not known what this system will decay to. However, if the closed string tachyon is localized around a spacetime singularity the endpoint of the decay process will often have the singularity resolved.

Tachyons in fiction

Tachyons appear in many works of fiction. It has been used as a standby mechanism upon which many science fiction authors rely to establish faster-than-light communication, with or without reference to causality issues. The word tachyon has become widely recognized to such an extent that it can impart a science-fictional "sound" even if the subject in question has no particular relation to superluminal travel (a form of technobabble, akin to positronic brain).

See also

• D-brane
• Massless particle
• Poincaré group
• Superbradyon, another class of hypothetical superluminal particles
• Tachyon condensation
• Tachyonic antitelephone

References

External links

• The Faster Than Light (FTL) FAQ (from the Internet Archive)
• "Tachyon" from Eric Weisstein's World of Physics
• Tachyon entry from the Physics FAQ