Rhombus
| Rhombus | |
|---|---|
 |
|
| Family | Bipyramid |
| Type | Quadrilateral |
| Edges and vertices | 4 |
| Symmetry group | D2 (*2) |
| Dual polygon | Rectangle |
| Properties | convex, Isotoxal |
In geometry, a rhombus or rhomb is a quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.
Every rhombus is a parallelogram, and a rhombus with right angles is a square. (Euclid's original definition and some English dictionaries' definition of rhombus excludes squares, but most modern mathematicians prefer the inclusive definition.)[1]
The English word “rhombus” derives from the Ancient Greek ῥόμβος (rhombos), meaning “spinning top”. The plural of rhombus can be either rhombi or rhombuses.
Contents |
Properties
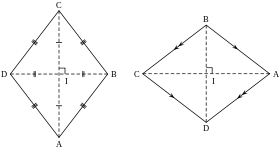
Every rhombus has two diagonals connecting opposite pairs of vertices and two pairs of parallel sides. Using congruent triangles, one can prove that the rhombus is symmetric across each of these diagonals. It follows that any rhombus has the following two properties:
- Opposite angles of a rhombus have equal measure.
- The two diagonals of a rhombus are perpendicular.
The first property implies that every rhombus is a parallelogram. A rhombus therefore has all of the properties of a parallelogram: opposite sides are parallel, adjacent angles are supplementary, and the two diagonals bisect one another.
Not every parallelogram is a rhombus, though any parallelogram with perpendicular diagonals (the second property) is a rhombus. In general, any quadrilateral with perpendicular diagonals, one of which is a line of symmetry, is a kite. Every rhombus is a kite, and any quadrilateral that is both a kite and parallelogram is a rhombus.
Origin
The word rhombus is from the Greek word for something that spins. Euclid used ρόμβος (rhombos), from the verb ρέμβω (rhembo), meaning "to turn round and round".[2][3] Archimedes used the term "solid rhombus" for two right circular cones sharing a common base.[4]
Rhombus in mathematics
- The dual polygon of a rhombus is a rectangle.
- One of the five 2D lattice types is the rhombic lattice, also called centered rectangular lattice.
- Identical rhombuses can tile the 2D plane in three different ways, including the Rhombille tiling.
- Three-dimensional analogues of a rhombus include the bipyramid and the bicone.
Area Formula
The area of a rhombus is "base times height" (as for a parallelogram)
or "base squared times the sine of any angle" (using the formula A=b2sinθ)
or "half the product of the diagonals" (using the formula A=½d1d2)
References
- ↑ Weisstein, Eric W., "Square" from MathWorld. inclusive usage
- ↑ Rhombos, "A Greek-English Lexicon", Liddel and Scott, at Perseus
- ↑ Rhembo, "A Greek-English Lexicon", Liddel and Scott, at Perseus
- ↑ http://www.pballew.net/rhomb.
External links
- Parallelogram and Rhombus - Animated course (Construction, Circumference, Area)
- Rhombus definition. Math Open Reference With interactive applet.
- Rhombus area. Math Open Reference Shows three different ways to compute the area of a rhombus, with interactive applet.