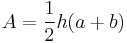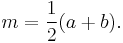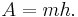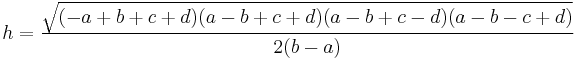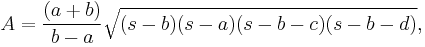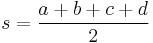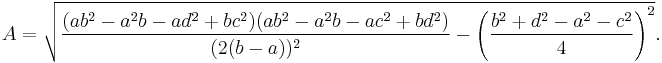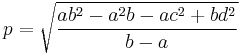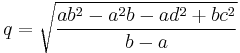Trapezoid

A trapezoid

In geometry, a four-sided figure with one pair of parallel sides is referred to as trapezoid in American English and as a trapezium in British English. A trapezoid with vertices ABCD is denoted Trapezoidn.PNG ABCD or ⏢ ABCD.

This article uses the term trapezoid in the sense that is current in the United States and some other English-speaking countries. Readers in the United Kingdom and Australia should read trapezium for each use of trapezoid in the following paragraphs.

The term trapezium has been in use in English since 1570, from Late Latin trapezium, from Greek trapezion, literally "a little table", diminutive of trapeza "table", itself from tra- "four" + peza "foot, edge". The first recorded use of the Greek word translated trapezoid (τραπεζοειδη, table-like) was by Marinus Proclus (412 to 485 AD) in his Commentary on the first book of Euclid’s Elements.[1]

There is also some disagreement on the allowed number of parallel sides in a trapezoid. At issue is whether parallelograms, which have two pairs of parallel sides, should be counted as trapezoids. Some authors[2] define a trapezoid as a quadrilateral having exactly one pair of parallel sides, thereby excluding parallelograms. Other authors[3] define a trapezoid as a quadrilateral with at least one pair of parallel sides, making the parallelogram a special type of trapezoid (along with the rhombus, the rectangle and the square).

Contents

Area

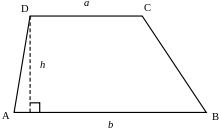
The area A of a trapezoid is given by[3]

A=\frac{1}{2}h(a + b)

where h is the height, and a and b are the lengths of the parallel sides. This yields as a special case the well-known formula for the area of a triangle, by considering a triangle as a degenerate trapezoid in which one of the parallel sides has shrunk to a point.

The mid-segment of a trapezoid is the segment that joins the midpoints of the non-parallel sides. Its length m is equal to the average of the lengths of the bases of the trapezoid:

m=\frac{1}{2}(a + b).

It follows that the area of a trapezoid is equal to the length of this mid-segment multiplied by the height:

A=mh.\,

In the case that the two parallel sides are different lengths (a ≠ b), the height of a trapezoid h, and hence its area A can be determined by the length of all of its sides:

h= \frac{\sqrt{(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}}{2(b-a)}

where, c and d are the lengths of the other two sides, and hence

A=\frac{a+b}{4(b-a)}\sqrt{(-a+b+c+d)(a-b+c+d)(a-b+c-d)(a-b-c+d)}.

When one of the parallel sides has shrunk to a point (say a = 0), this formula reduces to Heron's formula for the area of a triangle.

Another equivalent formula for the area, which more closely resembles Heron's formula is:

A = \frac{(a+b)}{b-a}\sqrt{(s-b)(s-a)(s-b-c)(s-b-d)},

where

s = \frac{a + b + c + d}{2}

is the semiperimeter of the trapezoid. (This formula is similar to Brahmagupta's formula, but it differs from it, in that a trapezoid might not be cyclic (inscribed in a circle). The formula is also a special case of Bretschneider's formula for a general quadrilateral).

Therefore using Bretschneider's formula gives:

A= \sqrt{\frac{(ab^2-a^2 b-ad^2+bc^2)(ab^2-a^2 b-ac^2+bd^2)}{(2(b-a))^2} - \left(\frac{b^2+d^2-a^2-c^2}{4}\right)^2}.

One can write expanded formulas for the area, but they are harder to remember because they have less symmetry.

Properties

In an isosceles trapezoid, the base angles have the same measure, and the other pair of opposite sides AD and BC also have the same length.

A quadrilateral is a trapezoid if and only if it has two adjacent angles that are supplementary, that is, they add up 180 degrees. Another necessary and sufficient condition is that the diagonals cut each other in mutually the same ratio (this ratio is the same as that between the lengths of the parallel sides).

The line joining the mid-points of the parallel sides bisects the area.

If the trapezoid above is divided into 4 triangles by its diagonals AC and BD, intersecting at O, then the area of ΔAOD is equal to that of ΔBOC, and the product of the areas of ΔAOD and ΔBOC is equal to that of ΔAOB and ΔCOD. The ratio of the areas of each pair of adjacent triangles is the same as that between the lengths of the parallel sides.

Therefore the diagonal length is

p= \sqrt{\frac{ab^2-a^2b-ac^2+bd^2}{b-a}}
q= \sqrt{\frac{ab^2-a^2b-ad^2+bc^2}{b-a}}

Confusing terminology

In North America and in Africa the term trapezium is sometimes defined as a quadrilateral with no parallel sides, though this shape is more usually called an irregular quadrilateral. The term trapezoid has been defined as a quadrilateral without any parallel sides in Britain and elsewhere,[4][5] but this does not reflect current usage (the Oxford English Dictionary says “Often called by English writers in the 19th century”).[6]

According to the Oxford English Dictionary, the sense of a figure with no sides parallel is the meaning for which Proclus introduced the term "trapezoid". This is retained in the French "trapézoïde", German "Trapezoid", and in other languages. A trapezium in Proclus' sense is a quadrilateral having one pair of its opposite sides parallel. This was the specific sense in England in 17th and 18th centuries, and again the prevalent one in recent use. A trapezium as any quadrilateral more general than a parallelogram is the sense of the term in Euclid. The sense of a trapezium as an irregular quadrilateral having no sides parallel was the usual sense in England from c1800 to c1875, but is now rare. This sense is the one that is standard in the U.S., but in practice quadrilateral is used rather than trapezium.[6]

The Temple of Dendur in the Metropolitan Museum of Art, New York

Architecture

In architecture the word is used to refer to symmetrical doors, windows, and buildings built wider at the base, tapering towards the top, in Egyptian style.

See also

References

  1. ↑ Oxford English Dictionary entry at trapezoid.
  2. ↑ "American School definition from "math.com"". http://www.math.com/school/glossary/defs/trapezoid.html. Retrieved 2008-04-14. 
  3. ↑ 3.0 3.1 ""Trapezoid" on MathWorld". http://mathworld.wolfram.com/Trapezoid.html. Retrieved 2010-01-28. 
  4. ↑ Chambers 21st Century Dictionary Trapezoid
  5. ↑ "1913 American definition of trapezium". Merriam-Webster Online Dictionary. http://www.merriam-webster.com/dictionary/trapezium. Retrieved 2007-12-10. 
  6. ↑ 6.0 6.1 Oxford English Dictionary entries for trapezoid and trapezium.

External links