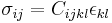Biomechanics

Biomechanics (from Ancient Greek: βίος "life" and μηχανική "mechanics"[1]) is the application of mechanical principles to living organisms, such as `humans, animals, plants and the functional basic units of life, the cells.[2] The word biomechanics developed during the early 1970s, describing the application of engineering mechanics to biological systems to solve medical problems by studying the function and structure of ”living organisms.” Mechanics is a branch of physics that involves the analysis of forces. Therefore biomechanics is the use of these principles to study the “anatomical and functional aspects”.[3]

Contents

Related fields

Biomechanics includes bioengineering, the research and analysis of the mechanics of living organisms and the application of engineering principles to and from biological systems. This research and analysis can be carried forth on multiple levels, from the molecular, wherein biomaterials such as collagen and elastin are considered, all the way up to the tissue and organ level. Some simple applications of Newtonian mechanics can supply correct approximations on each level, but precise details demand the use of continuum mechanics.

Chinstrap Penguin

The application of biomechanical principles to plants and plant organs has developed into the sister field of Plant biomechanics. The many strands of plant biomechanics are described in a text book on the subject by Karl Niklas Plant Biomechanics: An Engineering Approach to Plant Form and Function.

Applied mechanics, most notably thermodynamics and continuum mechanics, and mechanical engineering disciplines such as fluid mechanics and solid mechanics, play prominent roles in the study of biomechanics. By applying the laws and concepts of physics, biomechanical mechanisms and structures can be simulated and studied. Such concepts are found in the field of Sports Biomechanics where we apply the laws of mechanics and physics to human performance in order to gain a greater understanding of performance in athletic events through modeling, computer simulation and measurement. Elements of Mechanical Engineering (e.g. strain gauges), Electrical Engineering (e.g. digital filtering), Physics/Dynamics (e.g. moments of inertia), Computer Science (e.g. numerical methods) and Clinical Neurophysiology (e.g. surface EMG) are common methods used for the analysis.

Relevant mathematical tools include linear algebra, differential equations, vector and tensor calculus, numerics and computational techniques such as the finite element method.

The study of biomaterials is of crucial importance to biomechanics. For example, the various tissues within the body's organs, such as skin, bone, and arteries each possess unique material properties. The passive mechanical response of a particular tissue can be attributed to characteristics of the various proteins, such as elastin and collagen, living cells, ground substances such as proteoglycans, and the orientations of fibers within the tissue. For example, if human skin were largely composed of a protein other than collagen, many of its mechanical properties, such as its elastic modulus, would be different.

It has been shown that applied loads and deformations can affect the properties of living tissue. There is much research in the field of growth and remodeling as a response to applied loads. For example, the effects of elevated blood pressure on the mechanics of the arterial wall, the behavior of cardiomyocytes within a heart with a cardiac infarct, and bone growth in response to exercise, and the acclimative growth of plants in response to wind movement, have been widely regarded as instances in which living tissue is remodelled as a direct consequence of applied loads.

Chemistry, molecular biology, and cell biology have much to offer in the way of explaining the active and passive properties of living tissues. For example, in muscle contractions, the binding of myosin to actin is based on a biochemical reaction involving calcium ions and ATP.

History

Aristotle wrote the first book on biomechanics, De Motu Animalium, or On the Movement of Animals. He not only saw animals' bodies as mechanical systems, but pursued questions such as the physiological difference between imagining performing an action and actually doing it. Some simple examples of biomechanics research include the investigation of the forces that act on limbs, the aerodynamics of bird and insect flight, the hydrodynamics of swimming in fish, and locomotion in general across all forms of life, from individual cells to whole organisms. The biomechanics of human beings is a core part of kinesiology.

Applications

The study of biomechanics ranges from the inner workings of a cell to the movement and development of limbs, to the mechanical properties of soft tissue, and bones. As we develop a greater understanding of the physiological behavior of living tissues, researchers are able to advance the field of tissue engineering, as well as develop improved treatments for a wide array of pathologies.

Biomechanics is also applied in studying human muscleskeletion systems. In recent years, research applied force platform to study human joint reaction forces, 3D human movement. Human motion is also captured through the human Motion capture systems (e.g. Vicon systems) to study human 3D motion. With the help of force platform and vicon systems. It is possible to study the human muscleskeletion behavior, including joint reaction forces, human postural control etc. Research also applies Electromyography [4](EMG) system to study the muscle activation. By this, it is feasible to investigate the muscle responses to the external forces as well as perturbations.

Biomechanics is widely used in orthopedic industry to design orthopedic implants for human joints, dental parts, external fixations and other medical purposes. Biotribology is a very important part of it. It is a study of the performance and function of biomaterials used for orthopedic implants. It plays a vital role in order to improve the design and produce successful biomaterials for medical and clinical purposes.

Continuum mechanics

Human muscleskeletton system.

It is often appropriate to model living tissues as continuous media. For example, at the tissue level, the arterial wall can be modeled as a continuum. This assumption breaks down when the length scales of interest approach the order of the micro structural details of the material. The basic postulates of continuum mechanics are conservation of linear and angular momentum, conservation of mass, conservation of energy, and the entropy inequality. Solids are usually modeled using "reference" or "Lagrangian" coordinates, whereas fluids are often modeled using "spatial" or "Eulerian" coordinates. Using these postulates and some assumptions regarding the particular problem at hand, a set of equilibrium equations can be established. The kinematics and constitutive relations are also needed to model a continuum.

Second and fourth order tensors are crucial in representing many quantities in electromechanical. In practice, however, the full tensor form of a fourth-order constitutive matrix is rarely used. Instead, simplifications such as isotropy, transverse isotropy, and incompressibility reduce the number of independent components. Commonly-used second-order tensors include the Cauchy stress tensor, the second Piola-Kirchhoff stress tensor, the deformation gradient tensor, and the Green strain tensor. A reader of the mechanic's literature would be well-advised to note precisely the definitions of the various tensors which are being used in a particular work.

Biofluid Mechanics

Red blood cells

Under most circumstances, blood flow can be modeled by the Navier-Stokes equations. Whole blood can often be assumed to be an incompressible Newtonian fluid. However, this assumption fails when considering flows within arterioles. At this scale, the effects of individual red blood cells becomes significant, and whole blood can no longer be modeled as a continuum. When the diameter of the blood vessel is slightly larger than the diameter of the red blood cell the Fahraeus–Lindquist effect occurs and there is a decrease in wall shear stress. However, as the diameter of the blood vessel decreases further, the red blood cells have to squeeze through the vessel and often can only pass in single file. In this case, the inverse Fahraeus–Lindquist effect occurs and the wall shear stress increases.

Bones

Bones are anisotropic but are approximately transversely isotropic. In other words, bones are stronger along one axis than they are along a pivotal (i.e., normal or orthogonal) axis, and are approximately the same strength no matter how they are rotated around the one axis.

The stress-strain relations of bones can be modeled using Hooke's law, in which they are related by elastic moduli, e.g., Young's modulus, Poisson's ratio or the Lamé parameters. The constitutive matrix, a fourth-order tensor, depends on the isotropy of the bone.

\sigma_{ij}=C_{ijkl}\epsilon_{kl}

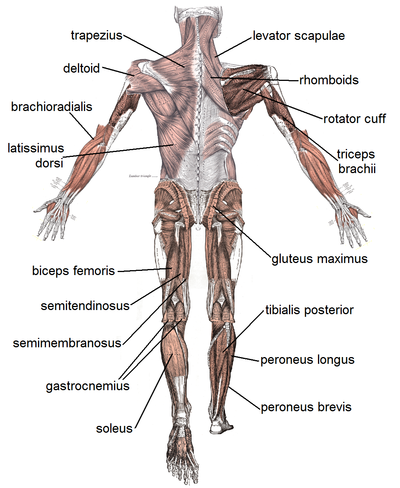
Muscle

There are three main types of muscles:

Soft tissues

Soft tissues such as tendon, ligament and cartilage are combinations of matrix proteins and fluid. In each of these tissues the main strength bearing element is collagen, although the amount and type of collagen varies according to the function each tissue must perform. Elastin is also a major load-bearing constituent within skin, the vasculature, and connective tissues. The function of tendons is to connect muscle with bone and is subjected to tensile loads. Tendons must be strong to facilitate movement of the body while at the same time remaining compliant to prevent damage to the muscle tissues. Ligaments connect bone to bone and therefore are stiffer than tendons but are relatively close in their tensile strength. Cartilage, on the other hand, is primarily loaded in compression and acts as a cushion in the joints to distribute loads between bones. The compressive strength of cartilage is derived mainly from collagen as in tendons and ligaments, however because collagen is comparable to a "wet noodle" it must be supported by cross-links of glycosaminoglycans that also attract water and create a nearly incompressible tissue capable of supporting compressive loads.

Recently, research is growing on the biomechanics of other types of soft tissues such as skin and internal organs. This interest is spurred by the need for realism in the development of medical simulation.

Viscoelasticity

Viscoelasticity is readily evident in many soft tissues, where there is energy dissipation, or hysteresis, between the loading and unloading of the tissue during mechanical tests. Some soft tissues can be preconditioned by repetitive cyclic loading to the extent where the stress-strain curves for the loading and unloading portions of the tests nearly overlap. The most commonly used model for viscoelasticity is the Quasilinear Viscoelasticity theory (QLV). In addition, soft tissues exhibit other viscoelastic properties, including creep, stress relaxation, and preconditioning.

Nonlinear theories

Hooke's law is linear, but many, if not most problems in biomechanics, involve highly nonlinear behavior, particularly for soft tissues. Proteins such as collagen and elastin, for example, exhibit such a behavior. Some common material models include the Neo-Hookean behavior, often used for modeling elastin, and the famous Fung-elastic exponential model. Non linear phenomena in the biomechanics of soft tissue arise not only from the material properties but also from the very large strains (100% and more) that are characteristic of many problems in soft tissues.

Biotribology

The main aspects of tribology are related with friction, wear and lubrication. When the two surfaces come in contact during motion i.e. rub against each other, friction, wear and lubrication effects are very important to analyze in order to determine the performance of the material. Biotribolgy is a study of friction, wear and lubrication of biological systems especially human joints such as hips and knees. For example, femoral component and tibial component of knee implant rub against each other during daily activity such as walking or stair climbing. If the performance of tibial component needs to be analyzed, the principles of biotribology are used to determine the wear performance of the implant and lubrication effects of synovial fluid. In addition, the theory of contact mechanics also becomes very important for wear analysis.

See also

Notes

  1. ↑ In Modern Greek the corresponding term is εμβιομηχανική (confer: Ελληνική Εταιρεία Εμβιομηχανικής/ Hellenic Society of Biomechanics), since βιομηχανική has the meaning of "industrial."
  2. ↑ R. McNeill Alexandera (2005) Mechanics of animal movement, Current Biology Volume 15, Issue 16, 23 August 2005, Pages R616-R619
  3. ↑ Hall, Susan J. Basic Biomechanics. Boston: McGraw-Hill Companies, Inc, 1999. Print.
  4. ↑ Muscles Alive: Their Functions Revealed

References

Further reading

External links

Major subfields of biology
Anatomy · Astrobiology · Biochemistry · Biomechanics · Biophysics · Bioinformatics · Biostatistics · Botany · Cell biology · Cellular microbiology · Chemical biology · Chronobiology · Conservation biology · Developmental biology · Ecology · Epidemiology · Evolutionary biology · Genetics · Genomics · Histology · Human biology · Immunology · Marine biology · Mathematical biology · Microbiology · Molecular biology · Mycology · Neuroscience · Nutrition · Origin of life · Paleontology · Parasitology · Pathology · Pharmacology · Physiology · Systems biology · Taxonomy · Toxicology · Zoology