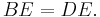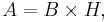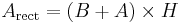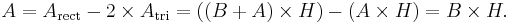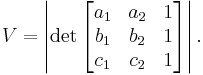Parallelogram

Parallelogram
This parallelogram is a rhomboid as its angles are oblique.
Type	Quadrilateral
Edges and vertices	4
Symmetry group	C₂ (2)

In geometry, a parallelogram is a quadrilateral with two pairs of parallel sides. In Euclidean Geometry, the opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean Parallel Postulate and neither condition can be proven without appealing to the Euclidean Parallel Postulate or one of its equivalent formulations. The three-dimensional counterpart of a parallelogram is a parallelepiped.

The etymology (in Greek παραλληλ-όγραμμον, a shape "of parallel lines") reflects the definition.

1 Properties
2 Types of parallelogram
3 Proof that diagonals bisect each other
4 The area formula
5 Computing the area of a parallelogram
6 See also
7 External links

Properties

Opposite sides of a parallelogram are equal in length.
Opposite angles of a parallelogram are equal in measure.
The area, 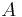$A$ , of a parallelogram is 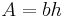$A = bh$ , where 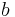$b$ is the base of the parallelogram and 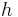$h$ is its height.
Opposite sides of a parallelogram will never intersect.
The area of a parallelogram is twice the area of a triangle created by one of its diagonals.
The area of a parallelogram is also equal to the magnitude of the vector cross product of two adjacent sides.
The diagonals of a parallelogram bisect each other.
Any non-degenerate affine transformation takes a parallelogram to another parallelogram.
There is an infinite number of affine transformations which take any given parallelogram to a square.
A parallelogram has rotational symmetry of order 2 (through 180°). If it also has two lines of reflectional symmetry then it must be a rhombus or a rectangle.
The perimeter of a parallelogram is 2(a + b) where a and b are the lengths of adjacent sides.

Types of parallelogram

Rhomboid - A quadrilateral whose opposite sides are parallel and adjacent sides are unequal, and whose angles are not right angles
Rectangle - A parallelogram with four angles of equal size (right angles).
Rhombus - A parallelogram with four sides of equal length.
Square - A parallelogram with four sides of equal length and four angles of equal size (right angles).

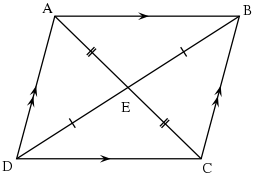
Proof that diagonals bisect each other

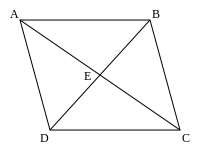
To prove that the diagonals of a parallelogram bisect each other, we will use congruent triangles:

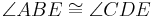$\angle ABE \cong \angle CDE$ (alternate interior angles are equal in measure)

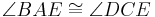$\angle BAE \cong \angle DCE$ (alternate interior angles are equal in measure).

(since these are angles that a transversal makes with parallel lines 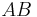$AB$ and $DC$ ).

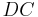Also, side AB is equal in length to side DC, since opposite sides of a parallelogram are equal in length.

Therefore triangles ABE and CDE are congruent (ASA postulate, two corresponding angles and the included side).

Therefore,

$AE = CE$

$BE = DE.$

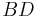Since the diagonals $AC$ and $BD$ divide each other into segments of equal length, the diagonals bisect each other.

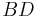Separately, since the diagonals $AC$ and $BD$ bisect each other at point 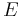$E$ , point 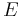$E$ is the midpoint of each diagonal.

The area formula

Area of the parallelogram is in blue

The area formula,

$A = B \times H,\,$

can be derived as follows:

The area of the parallelogram to the right (the blue area) is the total area of the rectangle less the area of the two orange triangles. The area of the rectangle is

$A_\text{rect} = (B+A) \times H\,$

and the area of a single orange triangle is

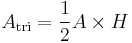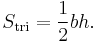
$A_\text{tri} = \frac{1}{2} A \times H\,$ or $S_\text{tri} = \frac{1}{2} bh.$

Therefore, the area of the parallelogram is

$A = A_\text{rect} - 2 \times A_\text{tri} = \left( (B+A) \times H \right) - \left( A \times H \right) = B \times H.\,$

Computing the area of a parallelogram

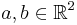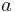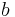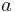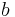Let $a,b\in\R^2$ and let $V=[a\ b]\in\R^{2\times2}$ denote the matrix with columns $a$ and $b$ . Then the area of the parallelogram generated by $a$ and $b$ is equal to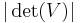 $|\det(V)|$

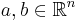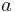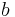Let $a,b\in\R^n$ and let $V=[a\ b]\in\R^{n\times2}$ Then the area of the parallelogram generated by $a$ and $b$ is equal to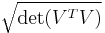 $\sqrt{\det(V^T V)}$

Let 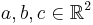$a,b,c\in\R^2$ . Then the area of the parallelogram with vertices at a, b and c is equivalent to the absolute value of the determinant of a matrix built using a, b and c as rows with the last column padded using ones as follows:

$V = \left| \det \begin{bmatrix} a_1 & a_2 & 1 \\ b_1 & b_2 & 1 \\ c_1 & c_2 & 1 \end{bmatrix} \right|.$

External links

Parallelogram and Rhombus - Animated course (Construction, Circumference, Area)
Weisstein, Eric W., "Parallelogram" from MathWorld.
Interactive Parallelogram --sides, angles and slope
Area of Parallelogram at cut-the-knot
Equilateral Triangles On Sides of a Parallelogram at cut-the-knot
Definition and properties of a parallelogram with animated applet
Interactive applet showing parallelogram area calculation interactive applet